Lab Notes for a Scientific Revolution (Physics)

April 4, 2009

Starting a new paper on Baryons and Confinement

Filed under: Baryons,Confinement,Current Density,Electrodynamics,Hadrons,Mesons,Nuclear Physics,Particle Physics,Physics,QCD,QED,Quantum Chromodynamics,Quantum Electrodynamics,Science,Uncategorized,Vector Potential,Yang Mills,Yang Mills Theory — Jay R. Yablon @ 11:49 pm

Today, I began work on a new paper dealing with the Yang-Mills foundations of baryons and QCD confinement.  The first draft is linked below, and I will provide updates as they develop.

Yang-Mills Foundations of Baryons and Confinement Phenomena

I may get diverted a bit by my US tax filing the next few days, and I am quite busy at work right now so this will mostly be a weekend and after-midnight project, but I do hope to get this paper, which I hope will synthesize many individual insights I have had and subjects I have studied over the past several years, into a something of value for others.

Constructive comments are always appreciated.

Thanks to the Princess and Peter and Ken and Igor and Ben for feedback and insights posted on the various newsgroups.

Jay.

March 22, 2008

A Possible Kaluza-Klein Experiment

Filed under: Compactification,Current Density,Electrodynamics,Experimental Physics,Fermions,Five Dimensions,Gravitation,Intrinsic Spin,Kaluza Klein,Maxwell Tensor,Non-Symmetric Field Theory,Physics,QED,Quantum Electrodynamics,Science,Spin Tensor,Vector Potential — Jay R. Yablon @ 3:31 pm

It has been suggested — appropriately so — that I consider whether there might be one or more experiments which can be designed to validate or falsify some of the Klauza-Klein results which I have been posting of late. I believe that one possible experiment resides in the non-symmetric energy tensor of trace matter derived in (11.6) of my latest posted paper. Thus, I have added a new section 15 to this paper, and reposted the entire paper, with this new section 15, at Kaluza-Klein Theory and Lorentz Force Geodesics Rev. 6.0 Because this is of particular interest as it may open some new experimental windows, I have posted section 15 below as well. Please note: the specific discussion of the connection between the compactified fifth dimension, and intrinsic spin, is not updated in this paper, and the latest discusssion I have written up on this topic, is at Intrinsic Spin and the Kaluza-Klein Fifth Dimension.

  Section 15: At this juncture, we have enough information to propose an experiment to validate or falsify some of the results derived thus far.  We turn for this purpose to the stress energy tensor of matter (11.6), which we raise into contravariant notation as follows:

\kappa T^{\nu \mu } =-\kappa \left(F^{\mu \tau } F^{\nu } _{\tau } -{\textstyle\frac{1}{4}} g^{\mu \nu } F^{\sigma \tau } F_{\sigma \tau } \right)+{\textstyle\frac{\sqrt{2} }{2}} \overline{\kappa }g^{5\mu } J^{\nu } =\kappa T^{\mu \nu } _{Maxwell} +{\textstyle\frac{\sqrt{2} }{2}} \overline{\kappa }g^{5\mu } J^{\nu } . (15.1)

The Maxwell tensor T^{\mu \nu } _{Maxwell} =T^{\nu \mu } _{Maxwell} is, of course, a symmetric tensor.  But the added trace matter term g^{5\mu } J^{\nu } is not necessarily symmetric, that is, there is no a priori reason why g^{5\mu } J^{\nu } must be equal to g^{5\nu } J^{\mu } .  The origin of this non-symmetry was discussed earlier in Section 9.

 With an eye toward conducting an experiment, let us now consider (15.1) in the linear approximation of (13.6) where {\rm L}_{QCD} \approx -A^{\beta } J_{\beta } -{\textstyle\frac{1}{4}} F^{\sigma \tau } F_{\sigma \tau } .  In the linear approximation, as used to reach (13.3), (12.11) reduces to g^{5\mu } \approx \overline{\kappa }\left(\frac{\phi ^{5\mu } -{\textstyle\frac{1}{2}} bA^{\mu } }{1+{\textstyle\frac{1}{2}} \overline{\kappa }\phi } \right)\approx -{\textstyle\frac{1}{2}} \overline{\kappa }bA^{\mu } , and (15.1) becomes:

T^{\nu \mu } \approx -\left(F^{\mu \tau } F^{\nu } _{\tau } -{\textstyle\frac{1}{4}} g^{\mu \nu } F^{\sigma \tau } F_{\sigma \tau } \right)-2J^{\nu } A^{\mu } =T^{\mu \nu } _{Maxwell} -2J^{\nu } A^{\mu } , (15.2)

where we have also used b^{2} =8 and 2\kappa =\overline{\kappa }^{2} , and divided out \kappa .  The transpose of this non-symmetric energy tensor is:

T^{\mu \nu } \approx -\left(F^{\mu \tau } F^{\nu } _{\tau } -{\textstyle\frac{1}{4}} g^{\mu \nu } F^{\sigma \tau } F_{\sigma \tau } \right)-2J^{\mu } A^{\nu } =T^{\mu \nu } _{Maxwell} -2J^{\mu } A^{\nu } , (15.3)

 Now, it is known that a non-symmetric energy tensor, physically, is indicative of a non-zero spin density.  In particular, using (15.2) and (15.3), the non-symmetry of the energy tensor is related to a non-zero spin density tensor S^{\mu \nu \alpha } according to: [A good, basic discussion of the spin tensor is at http://en.wikipedia.org/wiki/Spin_tensor.]

S^{\mu \nu \alpha } _{;\alpha } =T^{\mu \nu } -T^{\nu \mu } =-2J^{\mu } A^{\nu } +2J^{\nu } A^{\mu } . (15.4)

For such a non-symmetric tensor, the “energy flux” is not identical to the “momentum density, as these differ by (15.4), for \mu =0, \nu =k=1,2,3 and vice versa.  If the spin density S^{\mu \nu \alpha } =0, then  in this special case, (15.4) yields:

J^{\mu } A^{\nu } =J^{\nu } A^{\mu } . (15.5)

So, for S^{\mu \nu \alpha } =0, (15.3) may be written using (15.5) as the explicitly-symmetric tensor:

T^{\mu \nu } \approx -\left(F^{\mu \tau } F^{\nu } _{\tau } -{\textstyle\frac{1}{4}} g^{\mu \nu } F^{\sigma \tau } F_{\sigma \tau } \right)-J^{\mu } A^{\nu } -J^{\nu } A^{\mu } =T^{\mu \nu } _{Maxwell} -J^{\mu } A^{\nu } -J^{\nu } A^{\mu } . (15.6)

 Now, let’s consider a experiment which is entirely classical.  The T^{0k} “Poynting” components of (15.4), (15.6) represent the energy flux across a two-dimensional area, for a flux of matter which we will take to be a stream of electrons, while the T^{k0} components represent the momentum density.  The proposed experiment, then, will be to fire a stream of a very large number of electrons thereby constituting an electron “wave,” and to detect the aggregate flux of energy across a two-dimensional surface under various spin preparations, in precisely the same manner that one might test the flow of luminous energy across a surface when using light waves rather than electron waves.  Specifically, we propose in test I to fire electrons without doing anything to orient their spins, so that, statistically, the number of electrons flowing through the flux surface with positive helicity is equal to the number with negative helicity and so the spin density is zero, and (15.6) applies.  In test II, we fire electrons, but apply a magnetic field before detecting the flux, to ensure that all of the electrons are aligned to positive helicity.  In this event, the spin density, by design, is non-zero, and one of (15.2) or (15.3) will apply.  In test III, we do the same, but now apply the magnetic field to ensure that all of the electrons have negative helicity, before detecting the flux.

(more…)

March 6, 2008

Electrodynamic Potentials and Non-Linear QED in Kaluza-Klein

Filed under: Einstein Equation,Electrodynamics,Five Dimensions,General Relativity,Gravitation,Intrinsic Spin,Kaluza Klein,Physics,QED,Quantum Electrodynamics,Quantum Field Theory,Quantum Gravitation,Science,Unified Field Theory,Vector Potential — Jay R. Yablon @ 10:21 am

I have now added new sections 12, 13 and 14 to the Kaluza-Klein paper earlier posted.  These sections examine the relationship between the electrodynamic potentials and the gravitational potentials, and the connection to QED.  You may view this all at:

Electrodynamic Potentials and Non-Linear QED

Most significantly, these three new sections not only connect to the QED Lagrangian, but, they show how the familiar QED Lagrangian density

{\rm L}_{QCD} =-A^{\beta } J_{\beta } -{\textstyle\frac{1}{4}} F^{\sigma \tau } F_{\sigma \tau }

emerges in the linear approximation of 5-dimensional Kaluza-Klein gravitational theory.

Then, we go in the opposite direction, to show the QED Lagrangian density / action for non-linear theory, based on the full-blown apparatus of gravitational theory. 

Expressed in terms of the electrodynamic field strength F^{\sigma \tau } and currents J_{\beta }, this non-linear result is:

{\rm L}_{QCD} =0={\textstyle\frac{1}{8\kappa }} b\overline{\kappa }g^{5\beta } J_{\beta } -{\textstyle\frac{1}{4}} F^{\sigma \tau } F_{\sigma \tau } \approx -A^{\beta } J_{\beta } -{\textstyle\frac{1}{4}} F^{\sigma \tau } F_{\sigma \tau } , (13.6) 

where the approximation \approx shows the connection to the linear approximation.  Re-expressed solely in terms of the fifth-dimensional gravitational metric tensor components g_{5\sigma } and energy tensor source components T_{\beta 5}, this result is: 

\kappa {\rm L}_{QCD} =0={\textstyle\frac{1}{2}} g^{5\beta } \kappa T_{\beta 5} +{\textstyle\frac{1}{8}} g^{\sigma \alpha } \partial ^{\beta } g_{5\alpha } \left[\partial _{\sigma } g_{5\beta } -\partial _{\beta } g_{5\sigma } \right]. (14.4)

You may also enjoy the derivations in section 12 which decompose the contravariant metric tensor into gravitons, photons, and the scalar trace of the graviton. 

Again, if you have looked at earlier drafts, please focus on the new sections 12, 13 and 14.  Looking for constructive feedback, as always.

February 19, 2008

Lab Note 2 Progress Report: Draft Paper on Kaluza-Klein Theory and Lorentz Force Geodesics

Filed under: Chirality,Einstein Equation,Electrodynamics,Equivalence Principle,Five Dimensions,General Relativity,Geodesic,Gravitation,Gravitational Mass,Inertial Mass,Intrinsic Spin,Kaluza Klein,Mathematics,Maxwell Tensor,Maxwell's Equations,Nature,Particle Physics,Physics,QED,Quantum Electrodynamics,Quantum Field Theory,Quantum Gravitation,Science,String Theory,Technology,Uncategorized,Unified Field Theory,Vector Potential — Jay R. Yablon @ 11:27 pm

Hello to all my readers and contributors:

I have been very busy these past several days preparing my research on Kaluza-Klein five-dimensional theory into a formal paper.  I now have a draft paper sufficiently advanced, that I would like to share it with my readers and contributors for their comment.

I am not going to reproduce this directly on the blog as there are dozens of equations and the paper itself is already 25 pages.  However, I have linked a PDF copy of the latest draft below, for your perusal and comment.

Kaluza-Klein Theory and Lorentz Force Geodesics — 2-19-08 Draft

I know that there are literally dozens if not hundreds of Kaluza-Klein papers already out there in the world.  This one, I believe, is the one that actually describes how nature works, and how classical gravitation and electrodynamics actually do become united in nature.

Looking forward to your thoughts.

Jay. 

February 14, 2008

Lab Note 2, Part 3: Gravitational and Electrodynamic Potentials, the Electro-Gravitational Lagrangian, and a Possible Approach to Quantum Gravitation

Filed under: Einstein Equation,Electrodynamics,Five Dimensions,General Relativity,Geodesic,Gravitation,Mathematics,Maxwell Tensor,Maxwell's Equations,Nature,Physics,QED,Quantum Electrodynamics,Quantum Field Theory,Quantum Gravitation,Science,Technology,Unified Field Theory,Vector Potential — Jay R. Yablon @ 1:39 am

Note:  You may obtain a PDF version of Lab Note 2, with parts 2 and 3 combined, at Lab Note 2, with parts 2 and 3.

Also Note: This Lab Note picks up where Lab Note 2, Part 2, left off, following section 7 thereof.  Equation numbers here, reference this earlier Lab Note.

8.  The Electrodynamic Potential as the Axial Component of the Gravitational Potential

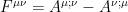 Working from the relationship F^{{\rm M} } _{{\rm T} } \propto 2\Gamma ^{{\rm M} } _{{\rm T} 5} which generalizes (5.4) to five dimensions, and recognizing that the field strength tensor F^{\mu \nu } is related to the four-vector potential A^{\mu } \equiv \left(\phi ,A_{1} ,A_{2} ,A_{3} \right) according to F^{\mu \nu } =A^{\mu ;\nu } -A^{\nu ;\mu } , let us now examine the relationship between A^{\mu } and the metric tensor g_{{\rm M} {\rm N} } .  This is important for several reasons, one of which is that these are both fields and so should be compatible in some manner at the same differential order, and not the least of which is that the vector potential A^{\mu } is necessary to establish the QED Lagrangian, and to thereby treat electromagnetism quantum-mechanically.  (See, e.g., Witten, E., Duality, Spacetime and Quantum Mechanics, Physics Today, May 1997, pg. 28.)

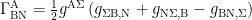 Starting with {\tfrac{1}{2}} F^{{\rm M} } _{{\rm T} } \propto \Gamma ^{{\rm M} } _{{\rm T} 5} , expanding the Christoffel connections \Gamma ^{{\rm A} } _{{\rm B} {\rm N} } ={\tfrac{1}{2}} g^{{\rm A} \Sigma } \left(g_{\Sigma {\rm B} ,{\rm N} } +g_{{\rm N} \Sigma ,{\rm B} } -g_{{\rm B} {\rm N} ,\Sigma } \right), making use of g^{{\rm M} {\rm N} } _{,5} =0 which as shown in (6.5) is equivalent to F^{{\rm M} {\rm N} } =-F^{{\rm N} {\rm M} } , and using the symmetry of the metric tensor, we may write:

{\tfrac{1}{2}} F^{{\rm M} } _{{\rm T} } \propto \Gamma ^{{\rm M} } _{{\rm T} 5} ={\tfrac{1}{2}} g^{{\rm M} \Sigma } \left(g_{\Sigma {\rm T} ,5} +g_{5\Sigma ,{\rm T} } -g_{{\rm T} 5,\Sigma } \right)={\tfrac{1}{2}} g^{{\rm M} \Sigma } \left(g_{5\Sigma ,{\rm T} } -g_{5{\rm T} ,\Sigma } \right).  (8.1)

It is helpful to lower the indexes in field strength tensor and connect this to the covariant potentials 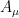A_{\mu } , generalized into 5-dimensions as A_{{\rm M} } , using F_{\Sigma {\rm T} } \equiv A_{\Sigma ;{\rm T} } -A_{{\rm T} ;\Sigma } , as such:

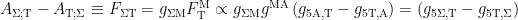A_{\Sigma ;{\rm T} } -A_{{\rm T} ;\Sigma } \equiv F_{\Sigma {\rm T} } =g_{\Sigma {\rm M} } F^{{\rm M} } _{{\rm T} } \propto g_{\Sigma {\rm M} } g^{{\rm M} {\rm A} } \left(g_{5{\rm A} ,{\rm T} } -g_{5{\rm T} ,{\rm A} } \right)=\left(g_{5\Sigma ,{\rm T} } -g_{5{\rm T} ,\Sigma } \right). (8.2)

The relationship 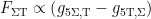F_{\Sigma {\rm T} } \propto \left(g_{5\Sigma ,{\rm T} } -g_{5{\rm T} ,\Sigma } \right) expresses clearly, the antisymmetry of F_{\Sigma {\rm T} } in terms of the remaining connection terms involving the gravitational potential.  Of particular interest, is that we may deduce from (8.2), the proportionality

A_{\Sigma ;{\rm T} } \propto g_{5\Sigma ,{\rm T} } . (8.3)

(If one forms A_{\Sigma ;{\rm T} } -A_{{\rm T} ;\Sigma } from (8.3) and then renames indexes and uses g_{{\rm M} {\rm N} } =g_{{\rm N} {\rm M} } , one arrives back at (8.2).)  Further, we well know that F_{\Sigma {\rm T} } =A_{\Sigma ;{\rm T} } -A_{{\rm T} ;\Sigma } =A_{\Sigma ,{\rm T} } -A_{{\rm T} ,\Sigma } , i.e., that the covariant derivatives of the potentials cancel out so as to become ordinary derivatives when specifying F_{\Sigma {\rm T} } , i.e., that F_{\Sigma {\rm T} } is invariant under the transformation A_{\Sigma ;{\rm T} } \to A_{\Sigma ,{\rm T} } .  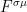Additionally, the Maxwell components (7.10) of the Einstein equation, are also invariant under A_{\Sigma ;{\rm T} } \to A_{\Sigma ,{\rm T} } , because (7.10) also employs only the field strength F^{\sigma \mu } .  Therefore, let is transform A_{\Sigma ;{\rm T} } \to A_{\Sigma ,{\rm T} } in the above, then perform an ordinary integration and index renaming, to write:

A_{{\rm M} } \propto g_{5{\rm M} } . (8.4)

In the four spacetime dimensions, this means that the axial portion of the metric tensor is proportional to the vector potential, g_{5\mu } \propto A_{\mu } , and that the field strength tensor F_{\Sigma {\rm T} } and the gravitational field equations -\kappa T^{{\rm M} } _{{\rm N} } =R^{{\rm M} } _{{\rm N} } -{\tfrac{1}{2}} \delta ^{{\rm M} } _{{\rm N} } R are invariant under the transformation A_{\Sigma ;{\rm T} } \to A_{\Sigma ,{\rm T} } used to arrive at (8.4).  We choose to set A_{\Sigma ;{\rm T} } \to A_{\Sigma ,{\rm T} } , and can thereby employ the integrated relationship (8.4) in lieu of the differential equation (8.3), with no impact at all on the electromagnetic field strength or the gravitational field equations, which are invariant with respect to this choice.

9.  Unification of the Gravitational and QED Lagrangians

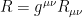 The Lagrangian density for a gravitational field in vacuo is {\rm L}_{gravitation} =\sqrt{-g} R, where g is the metric tensor determinant and R=g^{\mu \nu } R_{\mu \nu } is the Ricci tensor.  Let us now examine a Lagrangian based upon the 5-dimensional Ricci scalar, which we specify by:

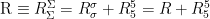{\rm R} \equiv R^{\Sigma } _{\Sigma } =R^{\sigma } _{\sigma } +R^{5} _{5} =R+R^{5} _{5} . (9.1)
(more…)

Blog at WordPress.com.